
Speel Futoshiki-puzzels online
In de volgende tutorial worden de basis- en geavanceerde technieken voor het oplossen van Futoshiki-puzzels stap voor stap gepresenteerd, met bijbehorende illustraties om de methoden op specifieke bordconfiguraties te laten zien.
Het uitgangspunt om tot een oplossing te komen is de definitie van het spel zelf: Futoshiki vereist dat de gebruiker een bord vindt waarop elk cijfer één keer op elke rij en kolom voorkomt, door de ongelijkheden op het bord te respecteren. Door dit criterium te gebruiken, kan vooruitgang worden geboekt door stap voor stap lege bordvierkanten met specifieke cijfers in te vullen, omdat dit de enige manier is om de beperkingen van het bord te respecteren.
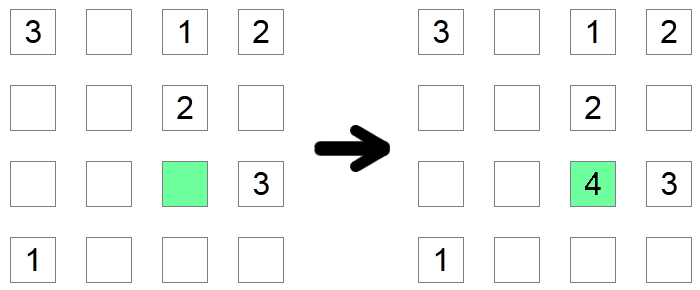
Als een vierkantje, kolom en rij al alle mogelijke cijfers bevatten, behalve één, dan moet dat vierkant het ontbrekende cijfer bevatten. In het bovenstaande voorbeeld moet het groene vierkant 4 zijn, omdat het geen andere waarde mag hebben omdat de andere mogelijke cijfers al in de rij of kolom van het veld staan.
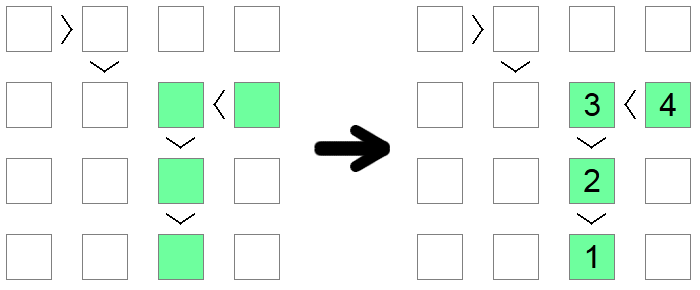
Als je een reeks ongelijkheden opmerkt, of het nu < (allemaal oplopend) of > (allemaal aflopend) is, gelijk aan de grootte van het bord, dan moet die ketting een reeks zijn van 1 tot aan de lengte van het bord. De lengte van de ketting garandeert dat deze sequentie de enige mogelijke oplossing is die voldoet aan de monotone toestand die wordt opgelegd door de ongelijkheidsketen.
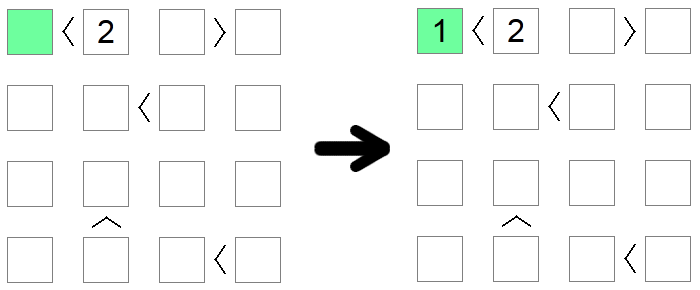
Vierkanten kleiner dan 2 moeten impliciet de waarde 1 hebben, aangezien dit de enige toegestane waarde op het bord is die aan deze voorwaarde voldoet. Evenzo moeten vierkanten die groter zijn dan de bordgrootte min 1 gelijk zijn aan de bordgrootte. In het voorbeeld hierboven is 1 de enige mogelijke waarde voor het groene vierkant (kleiner dan 2).
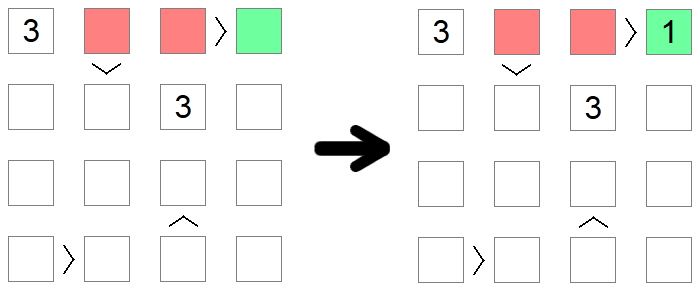
Vierkanten die groter zijn dan andere vierkanten mogen niet 1 zijn. Dit is de laagste waarde die op het bord is toegestaan, aangezien er geen kleinere waarde is dan 1. Op dezelfde manier kunnen vierkanten die lager zijn dan andere vierkanten niet de maximaal toegestane waarde bevatten, omdat er aan de andere kant van de ongelijkheid niets groter zou moeten worden ingevuld. In het bovenstaande voorbeeld kan 1 niet worden ingevuld in de rode vierkanten omdat ze allemaal groter zijn dan andere bordvierkanten, dus de enige mogelijke plaatsing voor 1 op de eerste rij van het bord is het groene vierkant.
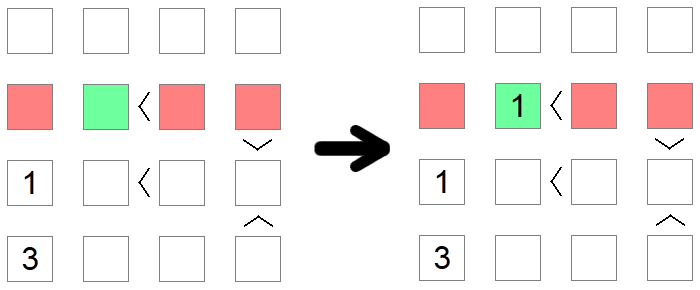
Soms moeten meerdere regels worden gebruikt om tot een conclusie te komen. Dit is het geval in het voorbeeld hierboven, waar we proberen de waarde 1 op de tweede rij van het bord te plaatsen. Het eerste rode vierkant is verwijderd vanwege een kolomuitsluiting (we hebben al een 1 in die kolom), terwijl het tweede en derde rode vierkantje worden verwijderd vanwege het uitsluiten van minimale waarden omdat aan die plaatsen meer dan de ongelijkheden zijn gekoppeld. Daarom blijft het groene vierkant de enige mogelijke plaats om 1 in die rij te plaatsen.
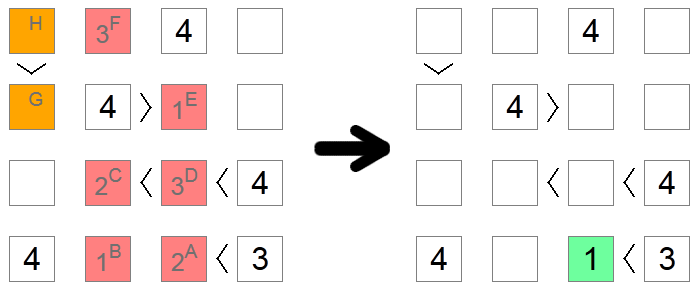
Soms zijn er, vooral op moeilijke borden, geen andere manieren om het juiste cijfer voor een vierkant te achterhalen, behalve door in de implicaties van elke mogelijkheid te duiken totdat een tegenstrijdigheid is bereikt. In het bovenstaande voorbeeld zijn alle rode en oranje vierkanten aanvankelijk leeg. We willen uitzoeken of het vierkant A 1 of 2 bevat. We gaan ervan uit dat het er 2 bevat en we kijken of we op basis van deze veronderstelling tot een tegenstrijdigheid komen.
Als vierkant A een 2 heeft, dan heeft vierkant B een 1 (de enige resterende waarde op de onderste rij). Vierkant C kan 1 of 2 zijn omdat het een keten van ongelijkheden heeft die vereist dat er 2 grotere getallen beschikbaar zijn, maar nu kan het niet 1 zijn vanwege de kolomuitsluiting van vierkant B, dus vierkant C is een 2 en vierkant D is een 3 (de enige waarde tussen 2 en 4). Vanwege kolomuitsluitingen is vierkant E gelijk aan 1 en vierkant F gelijk aan 3.
Als we nu naar de oranje vierkanten kijken, zien we de tegenstrijdigheid: als vierkant G 2 zou zijn, zou vierkant H ofwel 3 of 4 moeten zijn, wat niet is toegestaan vanwege een uitsluiting van een rij. Als vierkant G 3 zou zijn, zou vierkant H 4 moeten zijn, wat om dezelfde reden niet is toegestaan. Aangezien we geen resterende waarden meer hebben voor vierkant G, betekent dit dat we in een impasse zijn beland en dat onze aanvankelijke veronderstelling verkeerd was: 2 is geen geldige zet voor vierkant A, dus we kunnen er 1 in plaatsen, de enige andere mogelijke waarde.
We hebben hierboven laten zien hoe je een Futoshiki-puzzel met succes kunt oplossen door een reeks technieken te behandelen die je kunnen helpen de volgende zet te ontcijferen, zelfs in moeilijke situaties. Het andere belangrijke ingrediënt om vaardig en snel te worden in het oplossen van Futoshiki-puzzels is ervaring: hoe meer je oefent, hoe beter en sneller je wordt.
Als je zin hebt in een uitdaging, kun je nu een willekeurige Futoshiki-puzzel spelen door op de onderstaande knop te klikken. Veel succes!
© 2024 - Alle rechten voorbehouden - Over - Privacybeleid - DE | EN | ES | FR | IT | LV | NL | PL | PT | RO | SV | TR